SIFT特征点相对于ORB计算速度较慢,在没有GPU加速情况下,无法满足视觉里程计的实时性要求,或者无法运行在手机平台上,但是效果更好,精度更高。在应用时可以择优选取,了解其本质原理的动机是为了自己使用时,可以对其进行修改,针对自己的应用场景优化算法。
有足够的时间,可以去看D. Lowe的论文,理解起来更透彻.
1. 用高斯核构建尺度空间
对于构建的高斯金字塔,金字塔每层多张图像合称为一组(Octave),每组有多张(也叫层Interval)图像。通常高斯金字塔最底层为原始图像第0组,octave之间为降采样过程,对应OpenCV里的函数为PryDown()。注意这里降采样PryDown在直观上是金字塔向上走,要注意区分。
金字塔的第i组octave通过对第i-1组降采样获得(通常降采样的比例为2,也就是高斯模糊后去掉偶数行/列像素)。在每一组octave中还需要使用高斯核σ创建连续的尺度空间图像: σ, kσ, k2σ,..., kn-1σ,其中,k=21/s,s为每一组octave中再分的尺度层数。构建连续尺度空间的目的是为了提取特征点(角点)时,该特征点不仅在二维图像空间中是梯度极值点,还需要在第三维的尺度空间也是极值点。
当然,检测角点并不是直接在高斯卷积构建的尺度空间中,而是DoG(Difference of Gaussian)高斯差分尺度空间中,因此,为了保证DOG高斯差分尺度空间变化的连续性(是高斯卷积空间相邻尺度的差),需要在每一层octave的高斯卷积尺度首尾两边多创建一个尺度。
这里注意理解连续性,不是微积分里面的连续性,指的是尺度空间连续,(σ, kσ, k2σ,..., ks-1σ) ,(2σ, 2kσ, 2k2σ,..., 2ks-1σ) 。从这里可以看出,尺度空间主要由σ主导.
2. 在DoG尺度空间中检测极值点
虽然在高斯拉普拉斯LoG尺度空间中检测极值点是最精确的,但是由于计算量比较大,通常使用DoG尺度空间对其进行近似,在DoG尺度空间中进行局部最值搜索。有关LoG可以参考.LoG也就是将拉普拉斯算子作用于高斯核函数后形成的新的核函数,拉普拉斯算子的作用是求二阶偏导,对噪点响应较敏感,因此需要先用高斯核对图像进行平滑.
由于DoG尺度空间是离散的,我们只能通过比较DoG空间中某个点周围26个点来获取一个点是否可以作为极值(和ORB一样,这里可以选较少的几个先比较剔除).
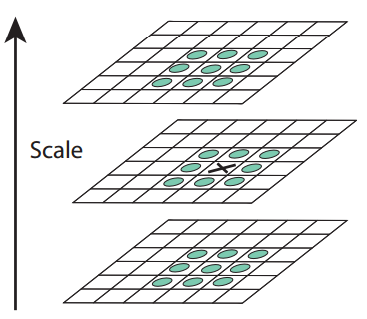
但是为了进一步获得精确的亚像素级别特征点位置,需要将DoG函数D(x,y,σ)在像素极值点附近二阶展开,对亚像素极值求偏导后=0求解.
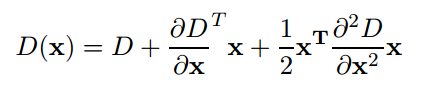
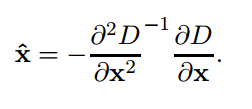
第二式带入第一式后可以得到亚像素极值点对应的DoG函数值,也就是对比度contrast:
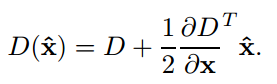
在检测到DoG尺度空间中的极值点(extremum)后,使用两个阈值来剔除质量不高(unstable)的点,contrastThreshold以及edgeThreshold.首先在DoG尺度空间中在potential的极值点附近二阶泰勒展开,寻找更精确的极值点坐标,其中,contrastThreshold是为了剔除对比度不高的极值点,edgeThreshold是为了剔除边缘点,因为边缘点也满足极值点的条件,但是不是需要的角点.
剔除对比度不高(不稳定)的点,|D(x)| < 0.03,这里假设DoG函数取值范围[0, 1].
剔除边缘点借鉴了Harris Corner的检测方法,计算特征点邻域的Hessian矩阵。
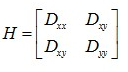
一次求导物理意义是变化率/梯度,二次求导物理意义是曲率,因此Hessian矩阵更能体现一个边缘的特征程度。
该Hessian矩阵的特征值代表了边缘特征的主曲率。两个特征值之间的比例体现了邻域两个垂直方向的曲率差别,这里去掉比例较大(横跨边缘和沿着边缘方向的曲率差别较大,>10)的点。注意这里不用特征值分解,而是用矩阵迹和行列式的性质,得到两个特征值比例就行.
3. 计算特征点方向
在检测到的特征点一个圆形邻域像素集合上计算各自的梯度幅值和梯度方向:
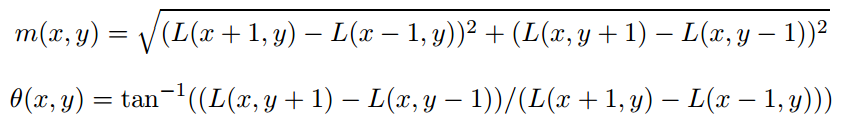
将360度方向划分为方向直方图中的36个bins,获取直方图的peak,作为特征点的方向。如果存在大于80%*peak幅值的方向,则在同一个尺度特征点(x,y,σ)上新建一个方向不同的特征点,有多少个新建多少个特征点.论文中说,相同位置的不会超过15%, 但是可以显著增强匹配的稳定性.注意这里的邻域是有区分度的,距离特征点近的像素在计算直方图时权重较大,使用高斯分布加权处理。
获得关键点主方向后,每个关键点有三个信息(x,y,σ,θ):位置、尺度、方向。
4. 计算128维描述子
在对邻域像素点采样前,要旋转xy坐标系和关键点的方向对齐,使得特征点具备方向不变的特征(旋转相机后,特征点描述子不变)。
计算128维空间中描述子的距离,SIFT的实现中计算的是欧氏距离.
练习:
OpenCV中提供的goodFeatureToTrack()可以使用Harris和Shi-Tomasi角点检测算法对图像进行角点提取,注意没有构建尺寸空间,且没有提供描述子计算,是最简单的角点提取算法,但是通过对其参数的调整,可以了解一些实现特点:
#include "common.h"#includeusing namespace std;using namespace cv;Mat origin, img;vector keyPoints;string title("FeatureDetector");int maxCorners(10);int qualityLevel(2);int minDistance(10);int blockSize(3);int useHarrisDetector(0);int k(4);int method(1);void detectCorner(int, void*);int main(){ origin = imread("/home/shang/dataset/opencv/building.jpg",CV_LOAD_IMAGE_COLOR); if(!origin.data){ cerr << "No data!"<< endl; return -1; } cvtColor(origin, img, CV_BGR2GRAY); namedWindow(title); createTrackbar("maxCorners", title, &maxCorners, 200, detectCorner); createTrackbar("qualityLevel (%)", title, &qualityLevel, 100, detectCorner); createTrackbar("minDistance", title, &minDistance, 400, detectCorner); createTrackbar("blockSize", title, &blockSize, 10, detectCorner); createTrackbar("useHarrisDetector", title, &useHarrisDetector, 1, detectCorner); createTrackbar("k when in HarrisDetector", title, &k, 100, detectCorner); createTrackbar("Method", title, &method, 2, detectCorner); detectCorner(0,0); imshow(title, img); while(true){ if(waitKey(0)==27) break; }}void detectCorner(int, void*){ Mat result ; img.copyTo(result); switch (method){ case 1: if(qualityLevel==0) { qualityLevel = 1; setTrackbarPos("qualityLevel (%)", title, 1); } if(blockSize==0) { blockSize = 1; setTrackbarPos("blockSize", title, 1); } goodFeaturesToTrack(result, keyPoints, maxCorners, qualityLevel/100.0, minDistance, noArray(), blockSize, useHarrisDetector, k/100.0 ); cvtColor(result, result, CV_GRAY2RGB); for(vector ::const_iterator it=keyPoints.begin(); it!=keyPoints.end(); it++){ circle(result, *it, 8, Scalar(0,0,255),2); } imshow(title, result); break; case 2: SiftFeatureDetector detector(100); vector keyPoints; detector.detect(result, keyPoints); cvtColor(result, result, CV_GRAY2RGB); for(vector ::const_iterator it=keyPoints.begin(); it!=keyPoints.end(); it++){ rectangle(result, Rect(it->pt.x-8,it->pt.y-8,16,16), Scalar(0,255,0),2); } imshow(title, result); break; } }
参考: